Azonnali érettségi: hány pontot kapnál matekból?
A koronavírus ellenére is úgy néz ki, május 4-én megkezdődnek az érettségik. Ráadásul március közepétől zárva az iskolák, így a felkészülés jóval nehezebb. Az Azonnalin úgy próbálunk segíteni, hogy az érettségik előtti héten naponta közzéteszünk egy-egy próbafeladatsort, amit az adott tárgy szakértői állítottak össze, és amivel tesztelheted, hogy állsz. Most a matekon a sor!

Pontosan egy hét múlva tartják a matematikaérettségit, ezért az Azonnalin most matekból próbálhatjátok ki magatokat.
Nem biztos, hogy jól járnátok, ha mi magunk állítjuk össze a feladatsort, így inkább felkértük rá Sándor András matematikust és matektanárt, aki az ELTE-n és Oxfordban végzett, most pedig a CEU-n kutat doktoranduszként, és mellette A Gondolkodás Öröme Alapítványnál tanít is.
A feladatsor formailag és témáiban megegyezik az érettségivel, viszont összességében jóval nehezebb, mint egy átlagos középszintű érettségi feladatsor. Többek között azért, mert
Így egyrészt nem érdemes az eredményéből messzemenő következtetéseket levonni, másrészt viszont tanulságos lehet a feladatok végiggondoldása. Mindenképp javasolt vizsgakörülmények között, írásban megoldani őket, mielőtt a megoldásokat elolvassátok.
+++
I. RÉSZ
Az itt található 12 rövid kérdés megoldására 45 perc áll rendelkezésre az érettségin. A megoldások sorrendje tetszőleges.
1. A={1,3,5,7,9}, B={2,3,4,5,6}
a) Add meg az A halmaz egy páros elemszámú részhalmazát, amelynek eleme az 5, de amely nem tartalmazza az 1-et!
b) Elemeinek felsorolásával add meg az .png) halmazt és az
halmazt és az 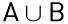 halmazt!
halmazt!
(3 pont)
Kattints az 1. feladat megoldásáért!
a) A következők bármelyike helyes: {5,3}, {5,7}, {5,9}, {5,3,7,9}. Az A halmaz elemeiből ki kell választanunk néhányat a megadottak szerint – csupán ennyit jelent ugyanis a részhalmaz fogalma. Érdemes a könnyű résszel kezdeni: tudjuk, hogy az 5-öt ki kell választani. És összesen páros darab kell nekünk. Ha nem akarunk kiszúrni magunkkal, legyen csak két darab. Az 1-et nem választhatom, bármi más jó. Például 5,7. És halmazként kell leírni a kiválasztott elemeket: {5,7}.
Érdemes megjegyezni, hogy egy halmaz elemeit bármilyen sorrendben megadhatjuk. A feladatban csak azért növekvő sorrendben vannak az elemek, mert így kényelmesebb velük dolgozni.
b) .png) = {1,7,9}
= {1,7,9}
Ezt a legegyszerűbben és legbiztosabban úgy kaphatjuk meg, ha leírjuk az A halmaz elemeit, majd végigmenvén a B halmaz elemein, ez utóbbiakat kihúzzuk a felsorolásból, amennyiben szerepelnek. Tehát esetünkben 1, 3, 5, 7, 9. A különbséghalmaz az így megmaradt elemekből áll.
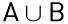 = {1,2,3,4,5,6,7,9}
= {1,2,3,4,5,6,7,9}
Ezesetben fel kell sorolni a két halmaz elemeit. Csupán arra kell figyelni, hogy semmi ne szerepeljen kétszer. A sorrend itt sem számít, bár könnyebb ellenőrizni magunkat, ha valamilyen logikus rendben soroljuk az elemeket.
2. Egyszerűsítsd az 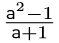 törtet, ha az a ismeretlen értéke nem -1.
törtet, ha az a ismeretlen értéke nem -1.
(2 pont)
Kattints a 2. feladat megoldásáért!
_1.png)
Ha szerencsénk van, eszünkbe jut, hogy van valami algebrai azonosság az _1.png) kifejezéssel. És ha nem sikerül pontosan felidézni, akkor esetleg a függvénytábla segíthet. A keresett azonosság:
kifejezéssel. És ha nem sikerül pontosan felidézni, akkor esetleg a függvénytábla segíthet. A keresett azonosság: 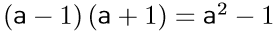 . Ebből egy osztással kijön a megoldás.
. Ebből egy osztással kijön a megoldás.
De mi van, ha ez nem jut eszünkbe? Ekkor nem szabad elkeseredni. Érdemes behelyettesíteni az a ismeretlen helyébe néhány egyszerű számot, és megnézni, mit kapunk. 0-ra a tört -1-et ad eredményül, 1-re 0-t, 2-re 1-et, 3-ra 2-t. Ebben megláthatjuk a szabály, hogy a tört értéke mindig eggyel kisebb, mint az a változó értéke, tehát 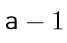 .
.
3. Egy mértani sorozat első tagja 400, hatodik tagja 12,5. Add meg a sorozat második tagját!
(2 pont)
Kattints a 3. feladat megoldásáért!
A megoldás: 200.
Mi történik egy mértani sorozatban? Mindig meg kell szorozni valamivel (ezt hívjuk hányadosnak vagy kvóciensnek) a sorozat tagjait, hogy a következő tagot kapjuk. Öt lépés alatt lesz 400-ból 12,5. Itt azt látjuk, hogy a számaink csökkennek, tehát egy egynél kisebb (abszolút értékű) szám lesz a hányados. Hányadrészére csökkent az öt lépésben, amíg az első tagtól a hatodikig jutunk? 400/12,5=32. Tehát öt lépés alatt 32-ed részére csökkent a szám. Így egy lépésben 2-vel kell osztani, hiszen 32=25. Vagyis a második tag 400/2=200.
A kevésbé intuitív, de mindig alkalmazható módszer – ami mindig működik, de kellemetlenebb a számolás – a következő: legyen q a hányados. Tudjuk, hogy a hatodik tag _1.png) . Így
. Így _1.png) . Vagyis
. Vagyis _1.png) a számológép segítségével. A második tag pedig
a számológép segítségével. A második tag pedig _1.png) .
.
Annyit érdemes még itt észben tartani, hogy általában egy mértani sorozat hányadosa lehet negatív szám is. De itt nem ez a helyzet.
4. Oldd meg a cos x = 0 egyenletet a valós számok halmazán!
(2 pont)
Kattints a 4. feladat megoldásáért!
A megoldás: _1.png) , ahol k egy tetszőleges egész szám (avagy
, ahol k egy tetszőleges egész szám (avagy _1.png) ).
).
Az ilyen típusú feladatoknál a legbiztosabb módszer az, ha felskicceljük magunknak a koszinuszfüggvény grafikonját, vagy kikeressük a függvénytáblából.
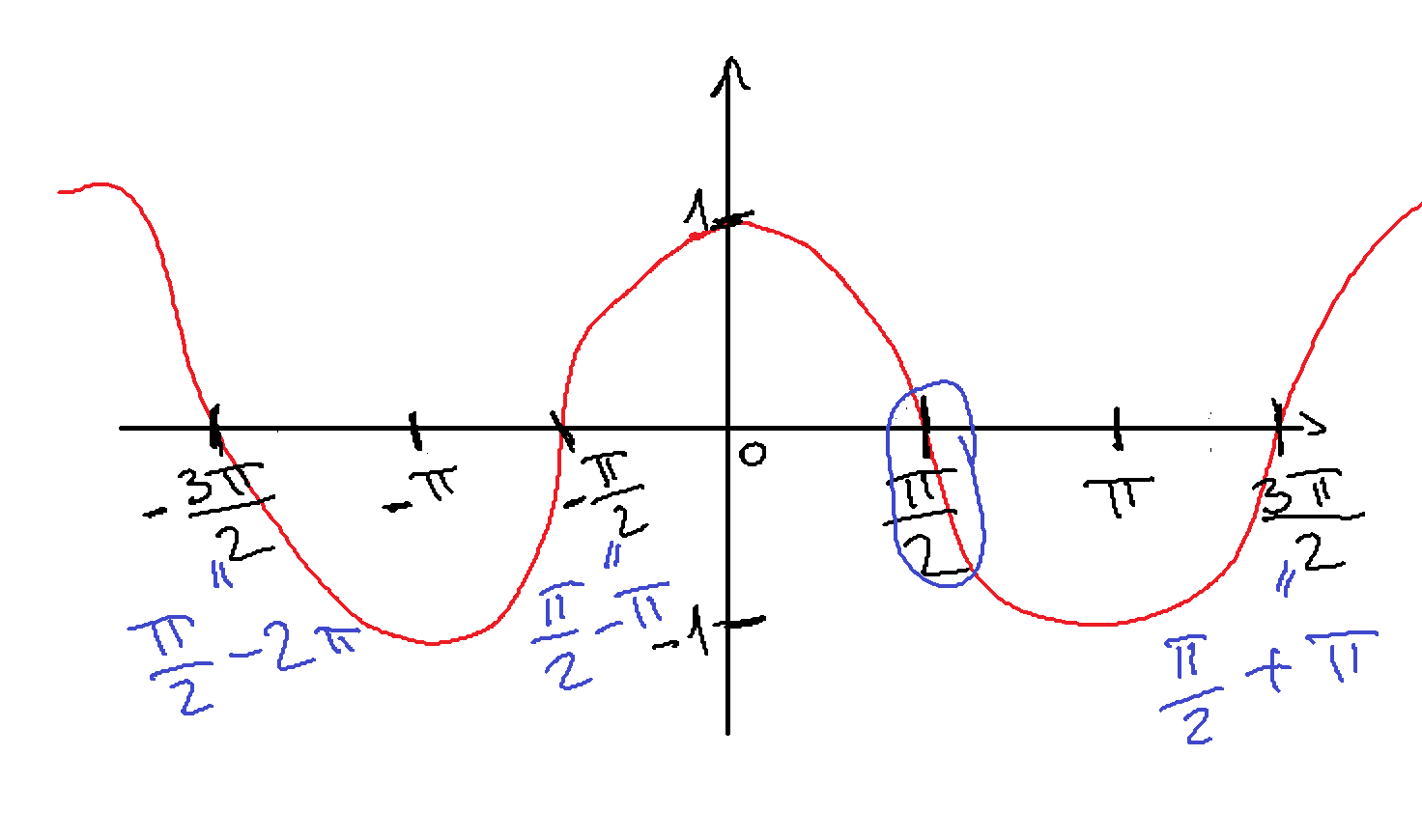
Az egyenlet az összes olyan x-et keresi, ahol a grafikon metszi az x tengelyt. Ezeket le tudjuk olvasni: az első ilyen hely a _1.png) , majd utána
, majd utána _1.png) -nként ismétlődik. Ezt az ismétlődést jelöljük a fenti „
-nként ismétlődik. Ezt az ismétlődést jelöljük a fenti „_1.png) ” módon az egyszerűség kedvéért.
” módon az egyszerűség kedvéért.
5. Egy 10-nél nagyobb, de 20-nál kisebb egész számnak 5 osztója van.
Mi lehet ez a szám? Válaszodat indokold!
(3 pont)
Kattints az 5. feladat megoldásáért!
A megoldás: 16.
Ha nincs ötletünk egy ilyen feladat megoldására, érdemes meggondolni, hogy végig lehet-e nézni az összes lehetőséget. 10 és 20 között 9 darab szám van összesen, tehát nagyon is végignézhető. Megkönnyíti a dolgunkat, ha felidézzük, hogy minden prímszámnak összesen két osztója van, és így ők nem jöhetnek itt szóba. A 9 számunk között négy prím van: 11, 13, 17, 19. Ezeket kizárhatjuk. A maradék öt szám osztói a következők:
12: 1,2,3,4,6,12;
14: 1,2,7,14;
15: 1,3,5,15;
16: 1,2,4,8,16;
18: 1,2,3,6,9,18
Egyszerűbb a megoldás, ha ismerjük azt a tényt, hogy egy számnak pontosan akkor van páratlan sok osztója, ha négyzetszám. (Különben egy szám osztóit osztópárokba lehet rendezni.) Így az egyetlen szóba jövő négyzetszám a 16, és elég ezt leellenőriznünk.
6. Egy bolti termék árát először 20%-kal emelték, majd később 40%-kal csökkentették. Hány százalékos egyszeri változásnak felel meg a két változtatás egymásutánja?
(2 pont)
Kattints a 6. feladat megoldásáért!
A megoldás: 28%-os csökkenés.
Gondolhatnánk, hogy a válasz egyszerűen +20%-40%, tehát -20%. De ez nem helyes, mert a második változtatás mértéke a 20%-os emelés utáni árhoz van viszonyítva, vagyis a megemelt ár 40%-ával kell csökkentenünk. A helyes módja a számolásnak az, ha a 20%-os emelést az ár 1,2-szeresére növekedésének fogjuk fel, a 40%-os csökkenést, 0,6-szorosára való csökkenésnek. Így azt kapjuk, hogy összességében az eredeti ár az 1,2∙0,6=0,72-szeresére változott. Ez pedig 28%-os csökkenésnek felel meg.
7. A 9x2+bx+1 másodfokú kifejezés diszkriminánsa 0. Add meg b lehetséges értékét/értékeit!
(3 pont)
Kattints a 7. feladat megoldásáért!
A megoldás: 6 és -6.
Egy ax2+bx+c másodfokú kifejezés diszkriminánsa b2-4ac. (Ez van a megoldóképletben a gyök alatt, és ezen múlik a megoldásszám.) Csak be kell helyettesíteni a képletbe, és meglátjuk, mi lesz. Esetünkben a=9, c=1, az ismeretlen b pedig itt is b. Így a diszkrimináns b2-4∙9∙1=b2-36. Ennek kell 0-nak lennie. Ne ijedjünk meg, ez egy nagyon egyszerű egyenlet. Átrendezve b2=36, innen b vagy 6 vagy -6.
8. Válaszd ki a megadott 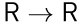 függvények közül a megfelelőket! (Egy függvény többször is szerepelhet.)
függvények közül a megfelelőket! (Egy függvény többször is szerepelhet.)
.png)
a) páros függvény(ek)
b) monoton növekvő függvény(ek)
(2 pont)
Kattints a 8. feladat megoldásáért!
A függvénytábla segítségével skicceljük fel a megadott függvényeket! Ez alapján megállapíthatjuk, hogy melyik hová való.
a) g és j. Egy függvény akkor páros, ha a grafikonja szimmetrikus az y tengelyre.
b) f. A másik háromban van csökkenő szakasz.
9. Az ábrán egy szabályos négyzetrács látható. Ezen bejelöltünk három vektort. Fejezd ki w-t u és v segítségével!
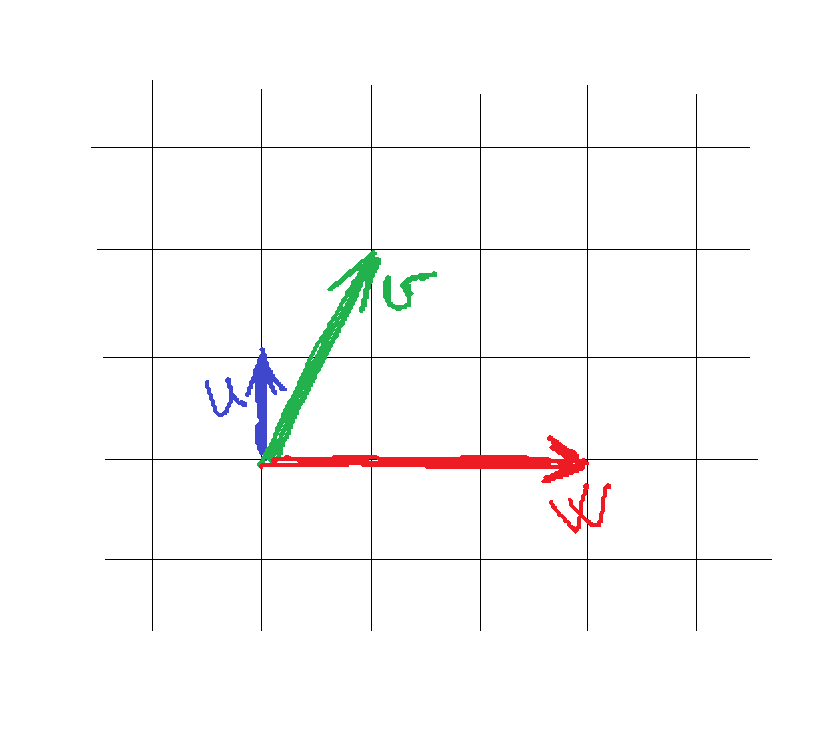
(3 pont)
Kattints a 9. feladat megoldásáért!
A megoldás: w=3v-6u
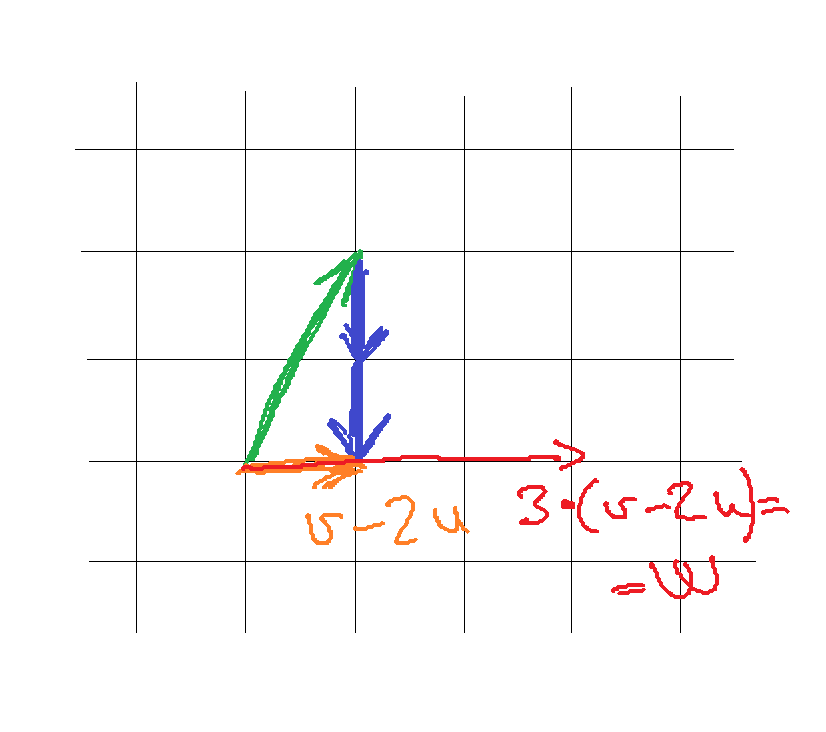
Ha vektorokat kell összeadnunk (ezt jelenti ugyanis, hogy fejezzük ki w-t a másik kettővel), akkor csak oda kell mozgatni gondolatban az egyik vektor kezdőpontját a másik végpontjához. Némi próbálkozás után kiderül, hogy sosem fogunk vízszintes vektort kapni u-ból és v-ből, mert mindkettő fölfelé mutat. Viszont a vektorok ellentettjét is használhatjuk, ha tudjuk, hogy kivonásnál csupán meg kell fordítani a vektorunkat. Így már tudunk vízszintes irányú vektort képezni: v-2u. Ennek éppen háromszorosa a keresett w. Így jön ki w=3(v-2u)=3v-6u.
10. Egy szabályos dobókockával kétszer dobunk. Mennyi a valószínűsége, hogy az első dobott szám kisebb, mint a második? Indokold!
(3 pont)
Kattints a 10. feladat megoldásáért!
A megoldás:  a valószínűség.
a valószínűség.
Összesen 36∙6=36 féle eredménye lehet a két dobásunknak (mindkét dobásra 6 lehetséges kimenetel), ezek egyenlő valószínűséggel fordulnak elő. A kérdés az, hogy közülük hány felel meg a feltételünknek?
Egy megoldási lehetőség, hogy szisztematikusan felsoroljuk az összes megfelelő számpárt:
(1,2), (1,3), (1,4), (1,5), (1,6)
(2,3), (2,4), (2,5), (2,6)
(3,4), (3,5), (3,6)
(4,5), (4,6)
(5,6)
Összesen 15 darab van. Így megkapjuk a fenti megoldást.
Egy másik lehetőség, hogy meggondoljuk, hogy a két dobás hogyan viszonyulhat egymáshoz. Lehetnek egyenlők, lehet az első nagyobb, vagy a második nagyobb. Egyenlőség 6 esetben áll fenn, mivel hatféle számot dobhatunk egy kockával. A maradék 36-6=30 eset pedig egyenlően oszlik el aszerint, hogy melyik dobás a nagyobb, mert a két dobás szerepe fölcserélhető. Így is megkapjuk a megoldást: 30/2=15.
11. Egy tízfős társaság összejövetelén mindenki pontosan 5 társával fogott kezet. Hány kézfogás történt összesen?
(2 pont)
Kattints a 11. feladat megoldásáért!
A megoldás: 25 kézfogás történik.
Ha nincs ötletünk, akkor ábrázolhatjuk gráfként a kézfogásokat. Kell 10 csúcs, és úgy húzzuk be az éleket, hogy mindegyikből 5 él induljon ki. Majd megszámolva az éleket 25-öt kapunk. Vigyázat, a számoláskor jelöljük be, hogy melyik élt számoltuk. És még így is könnyen elvéthetjük a leszámlálást.
A fenti módszer helyett elképzelhetjük, hogy hogyan számolnánk meg a kézfogásokat. Minden személy 5 kézfogásban vesz részt, és 10-en vannak. Tehát ez 50 kézfogás lenne. Viszont mindet kétszer számoltuk, mindkét résztvevő oldaláról egyszer-egyszer. Így kapjuk meg megoldást: _1.png) .
.
12. Add meg y értékét, ha 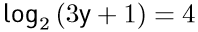 ! Megoldásod indokold!
! Megoldásod indokold!
(3 pont)
Kattints a 12. feladat megoldásáért!
A megoldás: y=5.
Egy lehetséges megoldási módszer, hogy a jobboldalt átírjuk egy 2-es alapú logaritmussá. A logaritmus azonosságai alapján _1.png) . Így a következőt kapjuk:
. Így a következőt kapjuk: _1.png) . Most lehagyhatjuk mindkét oldalról a logaritmust (a logaritmus monotonitása miatt), azt kapva, hogy
. Most lehagyhatjuk mindkét oldalról a logaritmust (a logaritmus monotonitása miatt), azt kapva, hogy _1.png) . Ebből y=(16-1)/3=5.
. Ebből y=(16-1)/3=5.
A megoldás első lépését a következő gondolattal is helyettesíthetjük: az egyenlet két oldala egyenlő, tehát ha a 2-t fölemelem a bal oldalon szereplő hatványra, az meg fog egyezni azzal, ha a jobb oldalon szereplő hatványra emelem. Tehát _1.png) . Az egyenlet bal oldala a logaritmus definíciója szerint 3y+1, a bal oldal pedig 16. A befejezés ugyanúgy, mint fent.
. Az egyenlet bal oldala a logaritmus definíciója szerint 3y+1, a bal oldal pedig 16. A befejezés ugyanúgy, mint fent.
+++
II. RÉSZ
Összetettebb feladatok következnek, a megoldások gondolatmenetén van a hangsúly, a pontok nagy része erre jár. A 13-15. feladatok megoldása kötelező, a 16-18. feladatok közül kettőt kell megoldani. Erre összesen 135 perc áll rendelkezésre az érettségin.
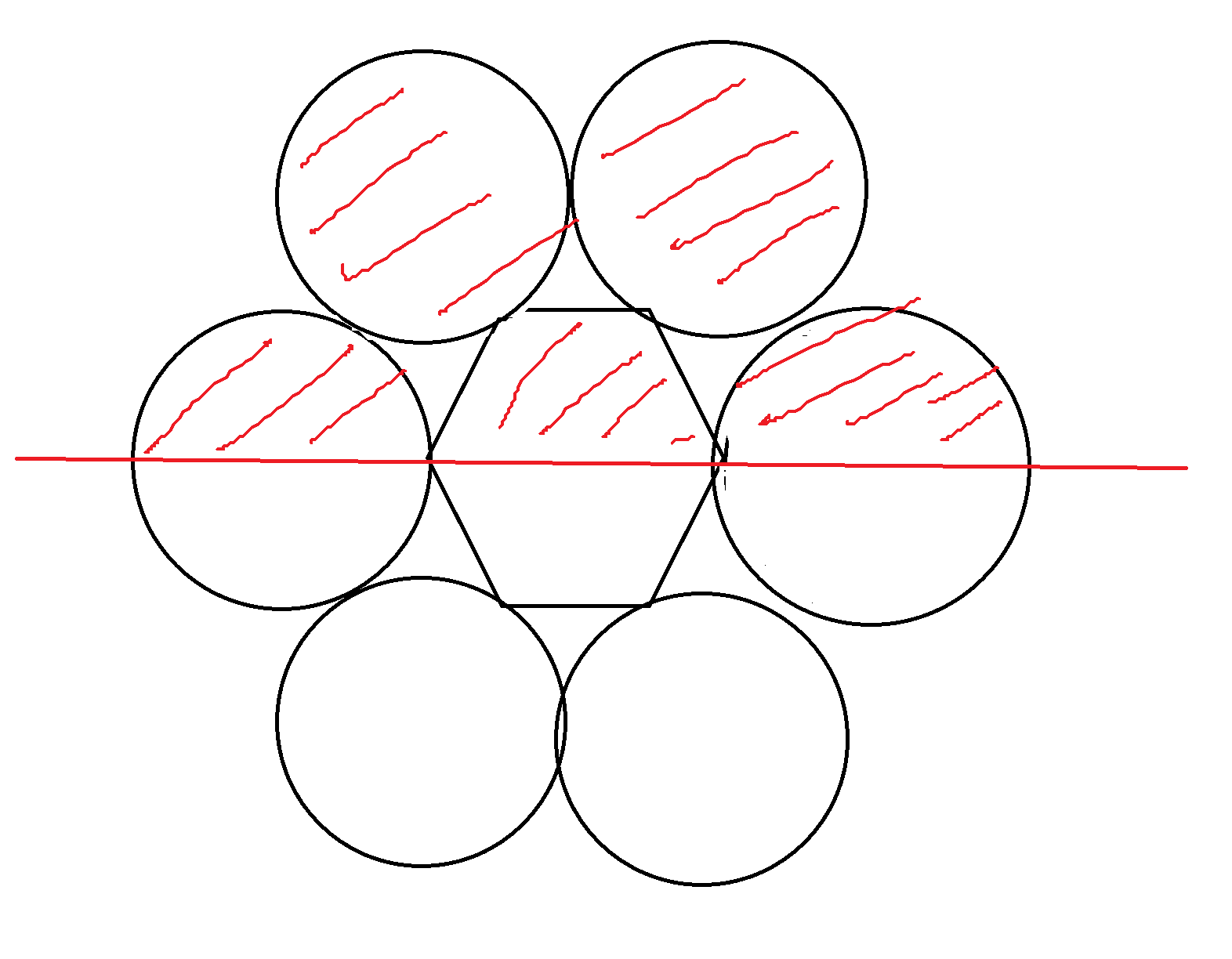
13. a) Egy gyártelepen 7 ipari épület található (az ábra felülnézetből mutatja őket). A központi épület szabályos hatszög alaprajzú, ennek oldala 40 m. A körülötte álló hat darab siló alapja egy-egy 40 m sugarú kör. Egy vihar megrongálta a telep északi felének tetőzetét (a vonal fölötti satírozott rész), így azt fel kell újítani. Mekkora a területe a felújítandó tetőrésznek?
b) Rajzolj egy gráfot a megadott csúcsokra, ahol minden csúcs fokszáma 4 vagy 5.

c) A fenti tulajdonságokkal legföljebb hány éle lehet egy gráfnak?
(a) 6 pont, b) 2 pont, c) 4 pont)
Kattints a 13. feladat megoldásáért!
a) A felújítandó tetőrész területe 17158,1 m2.
A kérdéses rész két teljes körből, két félkörből és a hatszög feléből tevődik össze. Elsőként számoljunk a körökkel! Egy kör területe _1.png) . A két félkör területe megegyezik egy teljes körével. Tehát összesen három kör területének összegére vagyunk kíváncsiak, ez
. A két félkör területe megegyezik egy teljes körével. Tehát összesen három kör területének összegére vagyunk kíváncsiak, ez _1.png) .
.
A hatszög felénél kétféleképpen is gondolkodhatunk. A hatszög középpontjából indulva, két vágással feldarabolhatjuk három egybevágó szabályos háromszögre, melyek oldala megegyezik a hatszög oldalával, tehát 40 m. A szabályos háromszög magassága _1.png) -szöröse az oldalának. Így a kis háromszögek területe egyesével
-szöröse az oldalának. Így a kis háromszögek területe egyesével _1.png) . A három háromszög együttesen pedig ennek háromszorosát teszi ki, azaz
. A három háromszög együttesen pedig ennek háromszorosát teszi ki, azaz _1.png) . Így a keresett terület összesen
. Így a keresett terület összesen _1.png) .
.
A hatszög felének területének kiszámolására egy másik természetes út is adódik. A hatszög behúzott felezővonala párhuzamos az oldalával, így a kapott idom egy trapéz. A trapéz alapjai 40m és 80m, magassága pedig _1.png) . A vonatkozó területképlet azonos eredményt ad a fentivel.
. A vonatkozó területképlet azonos eredményt ad a fentivel.
b) Egy példa a számos lehetőség közül:
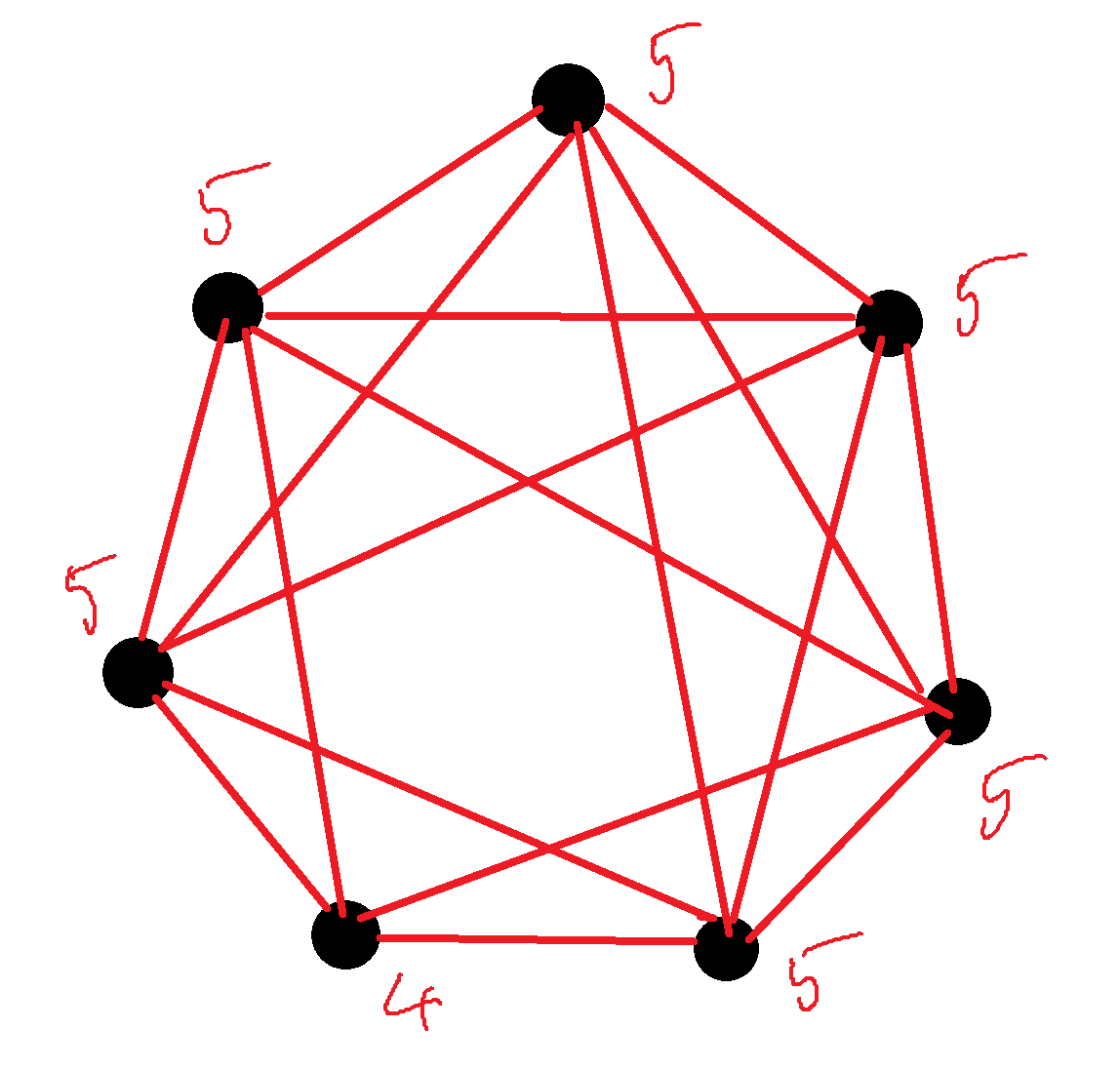
c) Legföljebb 17 éle lehet a gráfnak.
Egy gráf éleinek számát megkaphatjuk, ha összeadjuk a fokszámokat, majd az összeget elosztjuk kettővel (hiszen minden élt kétszer számoltunk). A lehető legnagyobb fokszámösszeg a megadott feltételekkel 7∙5=35-nek tűnik. Viszont a fokszámösszeg páros kell, hogy legyen minden gráfban (különben az élek száma nem volna egész), így a maximum 34. Ezzel pedig a számításunk 17 élt ad. Ez meg is valósítható, a fenti ábra egy jó példa rá.
14. Egy iskolai közvéleménykutatás során megkérdeztek 16 diákot, hogy hányszor ettek a büfében az elmúlt hónapban. A válaszok a következők voltak: 0,0,0,0,1,1,1,2,2,2,3,4,5,7,7,10.
a) Mennyi az adathalmaz mediánja, átlaga és szórása?
b) A büfében háromféle sütit lehet kapni: islert, zabkekszet és minyont. Egy 35 fős osztályban megkérdeztük, hogy ki melyiket szereti. Csak hárman voltak, akik egyiket sem jelölték meg a válaszokban, viszont nem volt olyan, aki a minyont és a zabkekszet is szereti. 24 olyan diák van, aki szereti legalább az egyiket, de nem a minyont. Hatan viszont csak a minyont szeretik. Hányan vannak, akik a minyont és az islert jelölték meg?
c) Egy csokimárka nyereményjátékot hirdet. Minden szelet csokival 5% nyerési esélyünk van. Ha 5 szeletet veszünk a boltban, mekkora esélyünk van arra, hogy van közte nyerő?
(a) 4 pont, b) 4 pont, c) 4 pont)
Kattints a 14. feladat megoldásáért!
a) A medián 2; az átlag 2,81; a szórás pedig 2,92.
A mediánt könnyedén kisilabizálhatjuk a nagyság szerint sorba rakott adatokból. A két középső szám 2 és 2, így a medián velük egyenlő. Az átlag is számolható úgy, hogy beütjük a számológépbe a számokat összeadva és elosztjuk 16-tal. De ez már sokkal egyszerűbb, ha a gép statisztikai funkcióját használjuk. A szórás esetében pedig rémálom egy ekkora adathalmazzal számolni. És még ha elméletileg teljesen képben is vagyunk, akkor is nagy eséllyel félreütünk valamit. Tehát ezt mindenképp a gép statisztika módjával számoljuk! Ha valakinek nincs olyan számológépe, amelynek a statisztikai funkcióját készségszinten ismeri, az gyorsan szerezzen be egyet és tanulja meg használni, mert ezen biztosan pontok múlnak az érettségin.
b) 2-en jelölték meg a minyont és az islert.
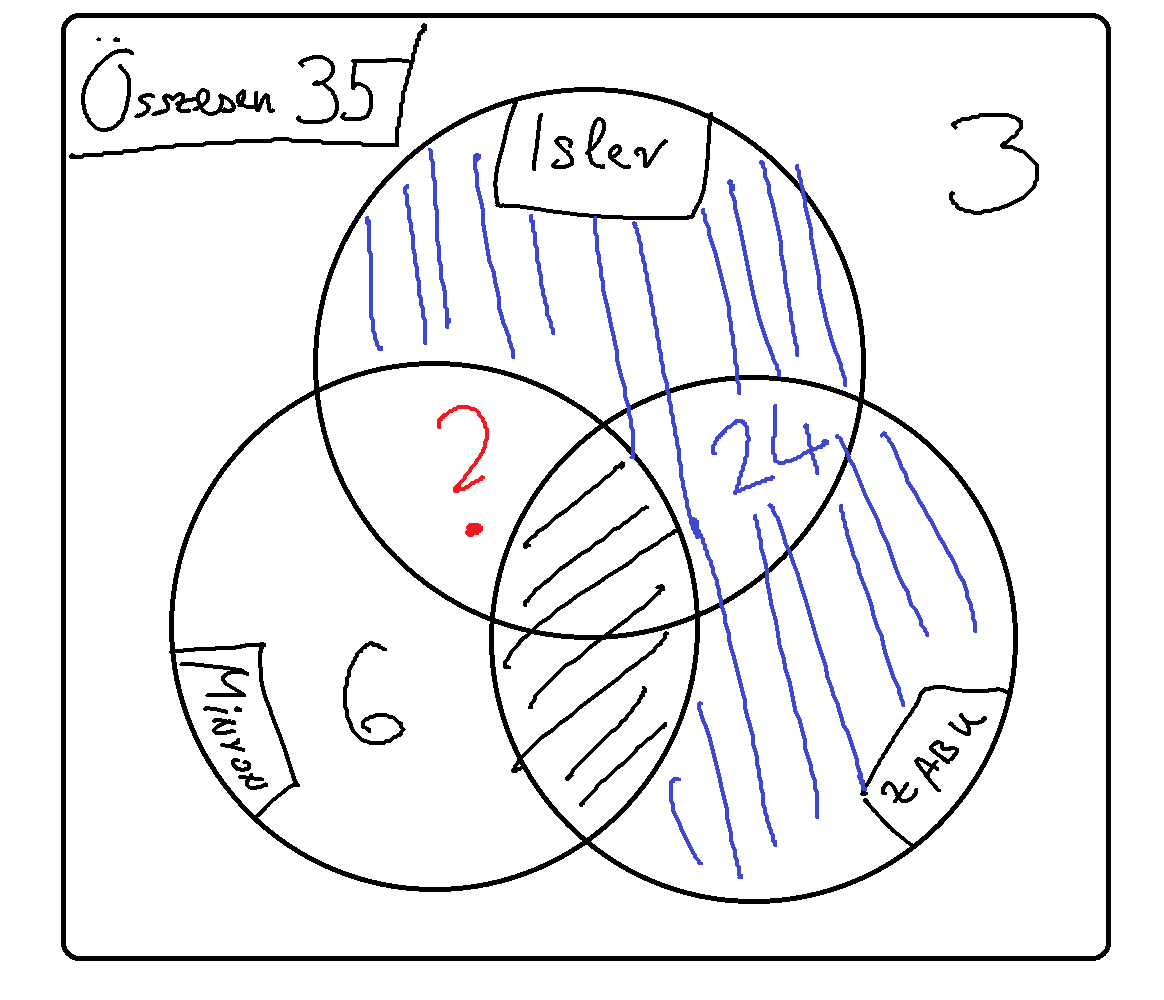
Ennek átlátásához mindenképp érdemes halmazábrát rajzolni. Ebbe beírhatjuk a megadott információkat. Kívül vannak 3-an, akik semmit sem szeretnek. A feketével satírozott rész, amely a zabkekszet és minyont szeretőkhöz tartozik, üres. A kékkel satírozott részben 24-en vannak összesen. A csak minyont szeretők pedig 6-an. Így a kimaradó, pirossal jelzett részbe kerül a maradék 35-3-24-6=2 diák.
c) 22,6% eséllyel van köztük nyerő.
Első pillantásra visszariaszthat bennünket, hogy végig kell nézni a binomiális valószínűségét annak, hogy egy, kettő, három, négy vagy öt csokival nyerünk. Szerencsére ebben nem kell elmerülnünk, mert áttérhetünk a komplementer eseményre, azaz megkérdezhetjük helyette, hogy mekkora az esélye annak, hogy egyik se nyer. Ez már könnyebbnek tűnik. Egy csoki esetén a nemnyerés esélye 95%, azaz 0,95. Így annak a valószínűsége, hogy az öt csokink egyike sem nyer, a csokikhoz tartozó nemnyerési esélyek szorzata. Ez pedig 0,955≈0,774. Így annak a valószínűsége, hogy legalább egy csokink nyer, ennek komplementere: 1-0,774=0,226, azaz 22,6%.
15.
a) Egy 8 cm átmérőjű, 20 cm magas egyenes körhenger alakú tolltartó palástját piros, két alapkörét pedig kék anyaggal szeretnénk beborítani. Mennyivel több piros anyagra van szükségünk, mint kékre (cm2-ben kifejezve)?
b) Oldd meg a valós számok körében az alábbi egyenletet!

c) Egy szabályos ötszög átlója 17 cm. Mekkorák az ötszög oldalai?
(a) 4 pont, b) 3 pont, c) 5 pont)
Kattints a 15. feladat megoldásáért!
a) 402,2 cm2-rel több piros anyagra van szükségünk.
Az egyenes körhenger palástjának területe felírható mint az alapkör kerülete szorozva a henger magasságával (kiolvasható a függvénytáblából, de egyébként szemléletesen is érthető). Így ez a terület, az adatainkat behelyettesítve _1.png) . A két alapkör területe pedig, a 4 cm-es sugárral számolva,
. A két alapkör területe pedig, a 4 cm-es sugárral számolva, _1.png) . A kettő különbsége adja a megoldást.
. A kettő különbsége adja a megoldást.
b) _1.png)
Az egyenlet elsőre ijesztőnek tűnhet, de valójában teljesen ártalmatlan, csupán egy furcsa formájú elsőfokú egyenlet. Vigyük át az x-es tagot jobbra és hozzunk közös nevezőre a jobb oldalon: _1.png)
5-tel leegyszerűsítve kapjuk a _1.png) , ahonnan, felszorozva 12-vel:
, ahonnan, felszorozva 12-vel: _1.png) .
.
c) Az oldal hossza 10,5 cm.
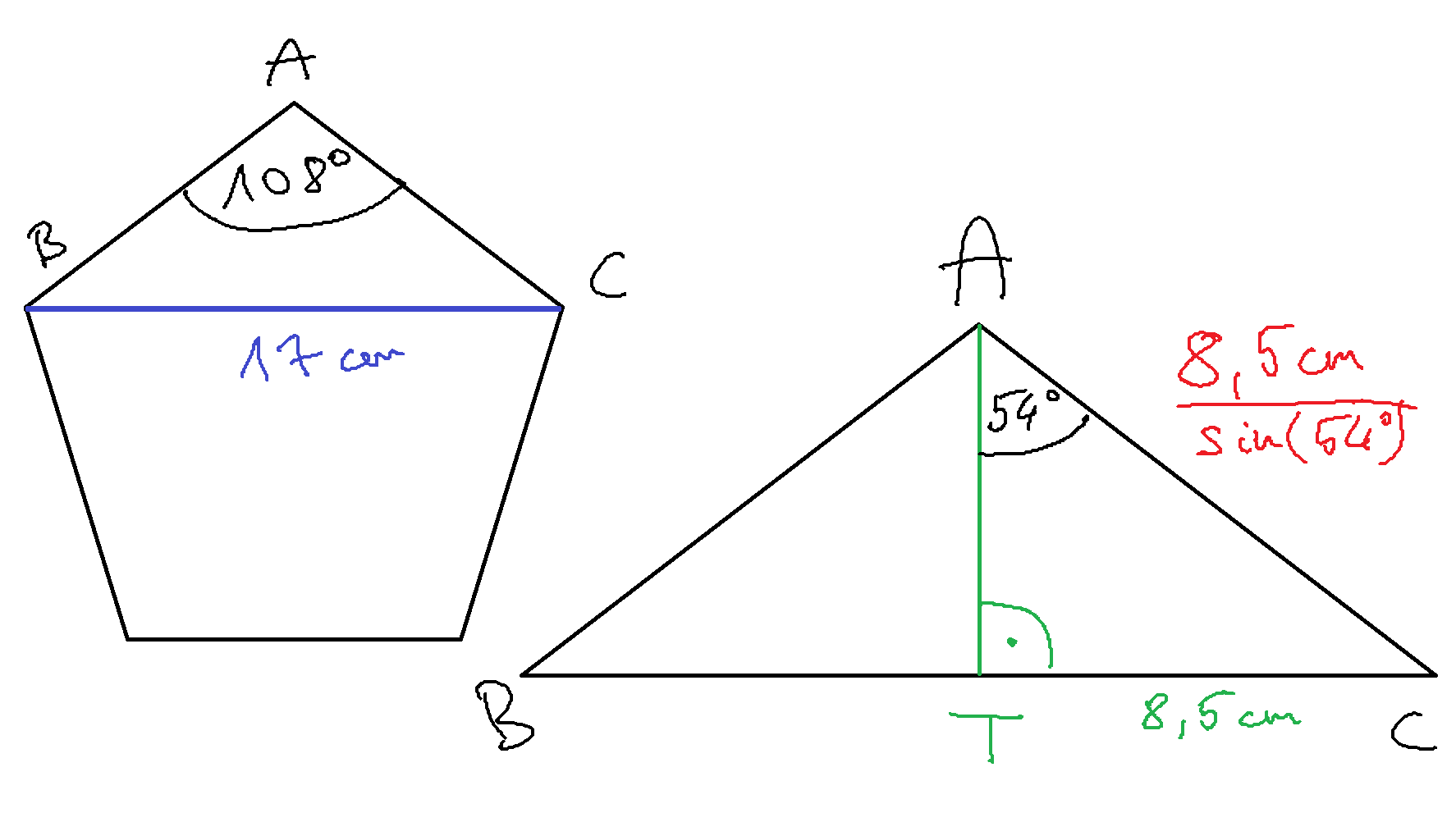
Az első ábrán látható szabályos ötszög átlója levág egy egyenlő szárú ABC háromszöget. Ennek A-nál lévő szöge 108°, amennyi a szabályos ötszög belső szögeinek mérete. Ha az A-hoz tartozó magasságot behúzzuk (talppontja T), akkor ez két egybevágó derékszögű háromszögre osztja ABC-t. A TC szakasz hossza 17cm/2=8,5cm. Az ezzel szemben lévő TAC szög pedig 108°/2=54°. Így a BC szakasz hossza, amely egyben az ötszög oldala is, felírható mint _1.png) . Az egyenlőszárú háromszögben szinusztételt is írhattunk volna az AC és BC oldalakra, ami ugyanezt az eredményt adja.
. Az egyenlőszárú háromszögben szinusztételt is írhattunk volna az AC és BC oldalakra, ami ugyanezt az eredményt adja.
16.
a) Oldd meg az alábbi egyenletet a valós számok halmazán:
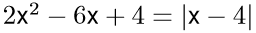
b) Az 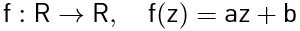 lineáris függvény zérushelye 3, a z=1 helyen pedig -4 az értéke. Ábrázold a függvényt és add meg a és b értékét!
lineáris függvény zérushelye 3, a z=1 helyen pedig -4 az értéke. Ábrázold a függvényt és add meg a és b értékét!
(a) 9 pont, b) 6 pont)
Kattints a 16. feladat megoldásáért!
a) Két megoldás van: x=0 és x=2,5.
Az abszolútértékes egyenletet szét kell választani: _1.png) és
és _1.png) . A terv: külön-külön megoldjuk őket és megnézzük, hogy értelmes megoldásokat kapunk-e. Mindkét egyenlet másodfokú. Az elsőnek a diszkriminánsa negatív, így nincs megoldása. A másodiknak két gyöke van x=0 és x=2,5. Visszahelyettesítve az eredeti abszolútértékes egyenletben azt kapjuk, hogy mindkettő teljesíti az egyenlőséget.
. A terv: külön-külön megoldjuk őket és megnézzük, hogy értelmes megoldásokat kapunk-e. Mindkét egyenlet másodfokú. Az elsőnek a diszkriminánsa negatív, így nincs megoldása. A másodiknak két gyöke van x=0 és x=2,5. Visszahelyettesítve az eredeti abszolútértékes egyenletben azt kapjuk, hogy mindkettő teljesíti az egyenlőséget.
b) a=2, b=-6
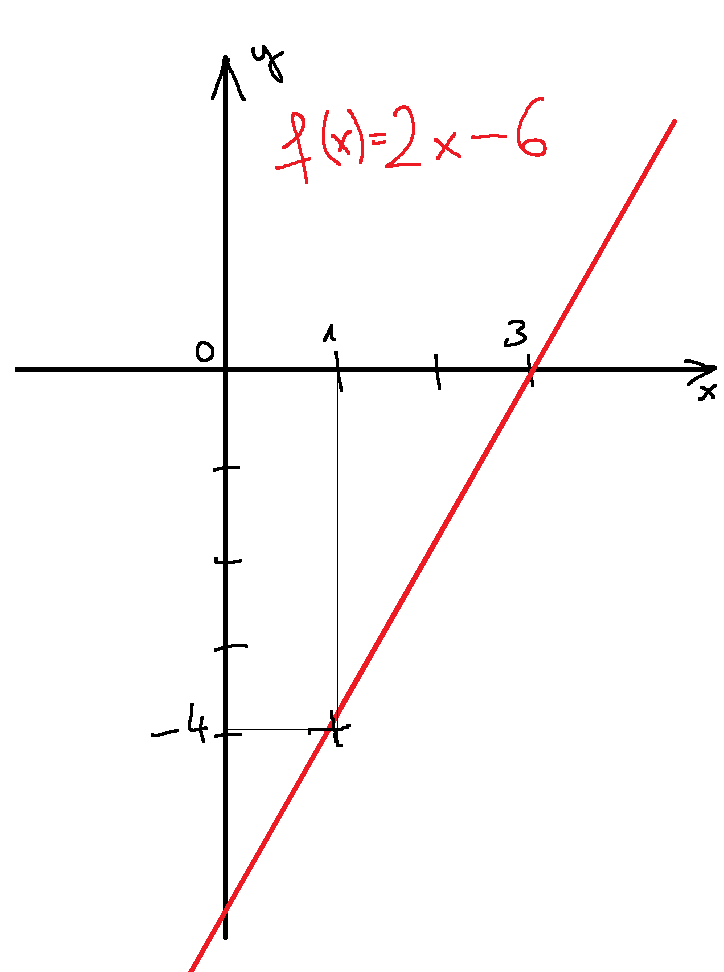
A függvény zérushelye azt jelenti, hogy a megadott értéket z-be helyettesítve 0-t ad a függvény. Ez esetünkben a következőt jelenti: _1.png) A másik feltétel hasonlóképpen ezt jelenti:
A másik feltétel hasonlóképpen ezt jelenti: _1.png) Van két ismeretlenünk: a és b, és van két lineáris egyenletünk, ez jó hír. Meg is tudjuk oldani: az elsőből a második egyenletet kivonva kapjuk, hogy 2a=4 (vigyázzunk az előjelekkel). Innen a=2 és b=-6.
Van két ismeretlenünk: a és b, és van két lineáris egyenletünk, ez jó hír. Meg is tudjuk oldani: az elsőből a második egyenletet kivonva kapjuk, hogy 2a=4 (vigyázzunk az előjelekkel). Innen a=2 és b=-6.
17. Adott az A(-1,2) és a B(1,5) pont a síkon.
a) Írd föl annak az A középpontú K körnek egyenletét, amely átmegy a B ponton!
b) Mik a koordinátái azon E és F pontoknak, ahol a K kör metszi az x tengelyt?
c) Írd föl a K körhöz az E és F pontokban húzott két érintőegyenletét!
(a) 4 pont, b) 3 pont, c) 6 pont)
Kattints a 17. feladat megoldásáért!
a) _1.png)
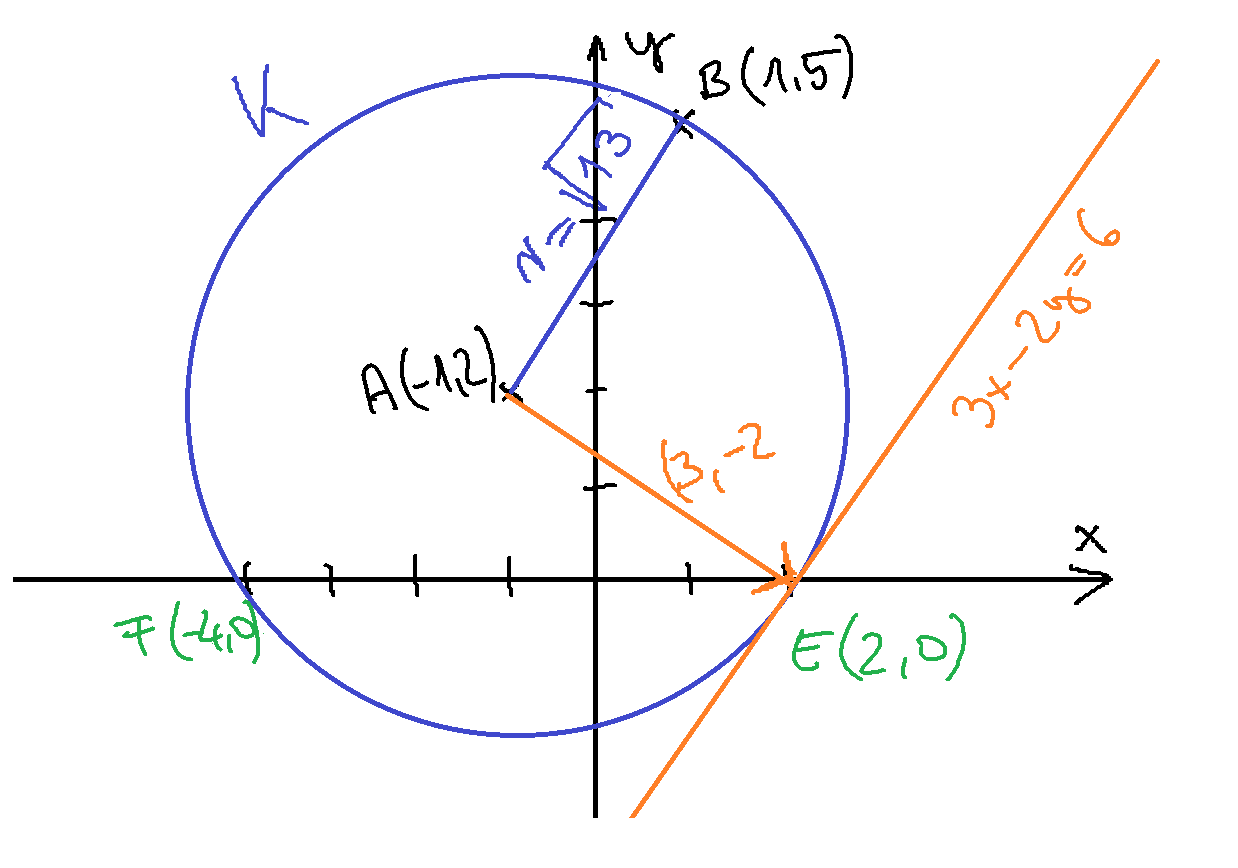
Készítsünk ábrát! A kör sugara Pithagorasz-tétellel _1.png) . A kör egyenlete pedig így
. A kör egyenlete pedig így _1.png) . Ellenőrizzük, hogy B koordinátái valóban teljesítik az egyenletet!
. Ellenőrizzük, hogy B koordinátái valóban teljesítik az egyenletet!
b) E(2,0) és F(-4,0)
Az x-tengelyt az határozza meg, hogy minden pontjának y koordinátája 0. Tehát a keresett metszéspontokat úgy kapjuk meg, ha a kör egyenletébe y=0-t helyettesítünk. Az így kapott egyenlet _1.png) . Átrendezve
. Átrendezve _1.png) . Ennek gyökei x=2 és x=-4. Így kapjuk a fenti E és F metszéspontokat.
. Ennek gyökei x=2 és x=-4. Így kapjuk a fenti E és F metszéspontokat.
c) 3x-2y=6 és -3x-2y=12
Érintőegyenletet úgy lehet a legegyszerűbben felírni, ha normálvektornak vesszük az érintési pontba mutató sugarat. Így az E-hez tartozó normálvektor (3,-2), az egyenes egyenlete ezzel a normálvektorral (úgy hogy tartalmazza E-t) pedig 3x-2y=6. Hasonlóképpen kaphatjuk meg az F-hez tartozó érintőegyenletét: -3x-2y=12.
18.
a) Egy házaspár két másik párt hív vendégségbe magához. Az ovális vacsoraasztalhoz hányféleképpen ülhetnek le, ha a párok egymás mellett akarnának ülni?
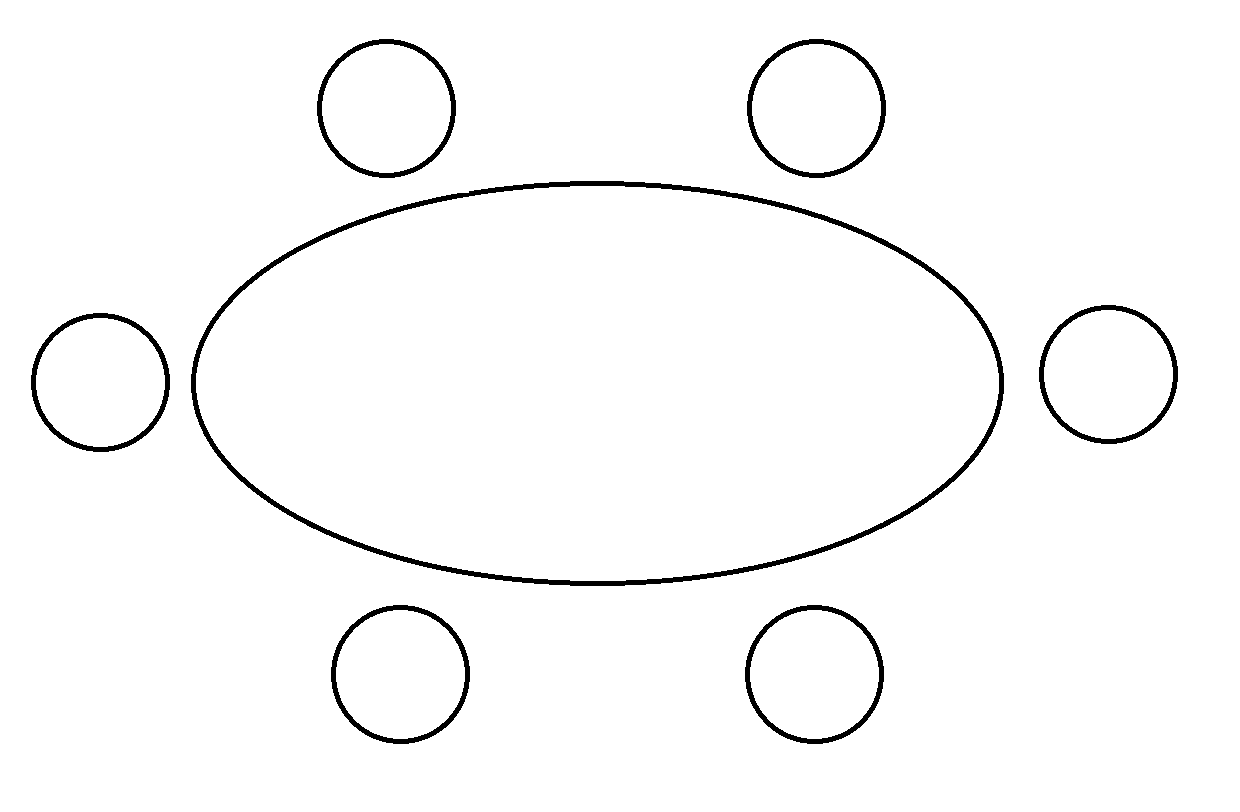
b) A fentiekkel ellentétben a két asztalfőt már elfoglalta a háziasszony és a házigazda. Hányféleképpen ülhet le most a másik két pár, ha megkérik őket, hogy a párok ne üljenek egymás mellé?
c) Egy radioaktív anyag felezési ideje két és fél nap. Órában és percben kifejezve mennyi idő alatt bomlik el az anyag 5%-a?
(a) 5 pont, b) 4 pont, c) 5 pont)
Kattints a 18. feladat megoldásáért!
a) 96-féleképpen foglalhatnak helyet párokban.
Sok különféle módon leszámlálhatjuk a lehetőségeket. De figyeljünk oda, hogy ne zavarodjunk bele abba, hogy körbeülik az asztalt!
Egy lehetséges végigszámolás a következő: jelöljünk ki egy főhelyet. Ide bármelyik ember ülhet a 6 közül. Mellé jobbra vagy balra kell ülnie a párjának. Ez eddig 6∙2 lehetőség. Ugyanabban az irányban tovább haladva a következő helyre ismét bárki ülhet: 4 lehetőség. Mellé muszáj a párját tenni: 1 lehetőség. A következő helyre megint 2 ember ülhet, és végül az utolsó helyre az utolsó ember. Ez összesen 6∙2∙4∙1∙2∙1=96. Jegyezzük meg, hogy nem számoltuk egyik ülésrendet sem többször.
b) 16-féleképpen
Az előzőhöz hasonlóan itt is sokféle logikával végig lehet gondolni. A fenti megoldás mintájára a következőt tehetjük: jelöljünk ki egy üres széket, erre bárki ülhet a 4 vendég közül. A helyet foglaló párja valahová a szembeoldalon kell, hogy üljön: ez 2 lehetőség. A fennmaradó két helyre a másik pár kétféleképpen ülhet le. Így helyes ülésrendet kapunk és minden ilyet egyszer számoltunk: 4∙2∙2=16.
c) 4 óra 26 perc alatt bomlik el az anyag 5%-a.
Váltsuk át rögtön a felezési időt órába: 60 óra. A radioaktív bomlás csökkenő exponenciális folyamat, így az atommagok Nt száma felírható a következőképpen: _1.png) , ahol N0 jelöli a kezdeti anyagmennyiséget, t az időt és μ a folyamatra jellemző konstanst. A felezési időből tudjuk, hogy
, ahol N0 jelöli a kezdeti anyagmennyiséget, t az időt és μ a folyamatra jellemző konstanst. A felezési időből tudjuk, hogy _1.png) . Keressük azt a T-t, amire
. Keressük azt a T-t, amire _1.png) . Mivel
. Mivel _1.png) , ezért 0,50,074=0,95 (a logaritmus definíciója szerint). Tehát a két egyenlet alapján
, ezért 0,50,074=0,95 (a logaritmus definíciója szerint). Tehát a két egyenlet alapján _1.png) . Aminek a két végét összeolvasva:
. Aminek a két végét összeolvasva: _1.png) . Ez pedig nagyjából 4 óra 26 perc.
. Ez pedig nagyjából 4 óra 26 perc.
Töltsd le a teljes feladatsort egyben ITT, a megoldókulcsot pedig ITT!
Szerdán a törivel folytatjuk! Ha kipróbálnád magad magyarból, ide kattints!
MONTÁZS: Vitárius Bence / Azonnali

Tetszett a cikk?

Az Azonnali hírlevele
Nem linkgyűjtemény. Olvasmány. A Reggeli fekete hétfőn, szerdán és pénteken jön, még reggel hét előtt – tíz baristából kilenc ezt ajánlja a kávéhoz!
Feliratkozásoddal elfogadod az adatkezelési szabályzatot.


